Introduction
Quantum gates are the building blocks of quantum computing. They are analogous to classical logic gates, but they operate on qubits instead of bits. Qubits exist in superpositions of two states, usually denoted as \(\ket{0}\) and \(\ket{1}\). Quantum gates can manipulate these states and create quantum phenomena such as entanglement and superposition.
In this article, I will review some of the most basic and common quantum gates, such as the Hadamard gate, the Pauli gates, the swap gate, the observation gate, and the CNOT gate. I will also show how they can be represented by matrices and applied to qubits.
Hadamard Gate
The Hadamard gate (H) is one of the most important quantum gates, as it can create superpositions of qubits. It is denoted with the H symbol in a box:

and the following matrix:
$$H = \frac{1}{\sqrt(2)} \begin{bmatrix}1 & 1 \\ 1 & -1\end{bmatrix} = \begin{bmatrix}\frac{1}{\sqrt(2)} & \frac{1}{\sqrt(2)} \\ \frac{1}{\sqrt(2)} & -\frac{1}{\sqrt(2)}\end{bmatrix}$$
The Hadamard gate transforms the qubit states as follows:
$$\ket{0} \to \begin{bmatrix}1 \\ 0\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt(2)} & \frac{1}{\sqrt(2)}\\ \frac{1}{\sqrt(2)} & -\frac{1}{\sqrt(2)}\end{bmatrix} = \frac{\ket{0}+ \ket{1}}{\sqrt(2)} \text{ , often denoted as } \ket{+}$$
$$\ket{1} \to \begin{bmatrix}0 \\ 1\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt(2)} & \frac{1}{\sqrt(2)}\\ \frac{1}{\sqrt(2)} & -\frac{1}{\sqrt(2)}\end{bmatrix} = \frac{\ket{0}- \ket{1}}{\sqrt(2)} \text{ , often denoted as } \ket{-}$$
Hadamard gate can also be used on a qubit that already is in a superposition. This operation will result in moving its state back to the initial state, for example:
$$\ket{-} = \frac{\ket{0}- \ket{1}}{\sqrt(2)} \to \begin{bmatrix}\frac{1}{\sqrt(2)} \\ -\frac{1}{\sqrt(2)}\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt(2)} & \frac{1}{\sqrt(2)}\\ \frac{1}{\sqrt(2)} & -\frac{1}{\sqrt(2)}\end{bmatrix} = \begin{bmatrix}0 \\ 1\end{bmatrix} = \ket{1}$$
Pauli X Gate
The Pauli X gate (or simply X-gate) is used to invert the state of the qubit. It might therefore be considered a quantum version of the classical NOT gate. It is denoted with the symbol:
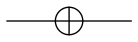
It takes the form of the following matrix:
$$X=\begin{bmatrix}0 \ 1 \\ 1 \ 0\end{bmatrix}$$
If the qubit has one of the elementary values, it will be inverted:
$$\ket {0} \to \begin{bmatrix}1 \ 0\end{bmatrix} \begin{bmatrix}0 \ 1 \\ 1 \ 0\end{bmatrix} = \begin{bmatrix}0 \\ 1\end{bmatrix} = \ket{1}$$
$$\ket {0} \to \begin{bmatrix}0 \\ 1\end{bmatrix} \begin{bmatrix}0 \ 1 \\ 1 \ 0\end{bmatrix} = \begin{bmatrix}1 \\ 0\end{bmatrix} = \ket{0}$$
If the qubit is in the superposition state, the probabilities will be inverted:
$$\frac{2}{3}\ket{0}+\frac{\sqrt(5)}{3}\ket{1} \to \begin{bmatrix}\frac{2}{3} \\ \frac{\sqrt(5)}{3}\end{bmatrix} \begin{bmatrix}0 \ 1 \\ 1 \ 0\end{bmatrix} = \begin{bmatrix} \frac{\sqrt(5)}{3} \\ \frac{2}{3}\end{bmatrix} = \frac{\sqrt(5)}{3}\ket{0}+\frac{2}{3}\ket{1}$$
Obviously, when the probabilities are 50/50, using the X-gate will not have an effect.
Pauli Y Gate
The Pauli Y gate (also called Y-gate) is denoted with the symbol:

and is represented by the matrix:
$$\begin{bmatrix} 0 \ -i \\ i \ 0 \end{bmatrix}$$
Applying Y-gate to elementary states gives:
$$\ket{0} \to \begin{bmatrix}1 \\ 0\end{bmatrix} \begin{bmatrix} 0 \ -i \\ i \ 0 \end{bmatrix} = \begin{bmatrix}0 \\ i\end{bmatrix} = i\ket{1}$$
$$\ket{1} \to \begin{bmatrix}0 \\ 1\end{bmatrix} \begin{bmatrix} 0 \ -i \\ i \ 0 \end{bmatrix} = \begin{bmatrix}-i \\ 0\end{bmatrix} = -i\ket{0}$$
Pauli Z Gate
The Pauli Z gate (also called Z-gate) leaves |0> state intact and flips |1> state. It is denoted with the symbol:
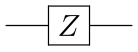
and is represented by the matrix:
$$\begin{bmatrix} 1 \ 0 \\ 0 \ -1 \end{bmatrix}$$
Applying Z-gate to elementary states gives:
$$\ket{0} \to \begin{bmatrix}1 \\ 0\end{bmatrix} \begin{bmatrix} 1 \ 0 \\ 0 \ -1 \end{bmatrix} = \begin{bmatrix}1 \\ 0\end{bmatrix} = \ket{0}$$
$$\ket{1} \to \begin{bmatrix}0 \\ 1\end{bmatrix} \begin{bmatrix} 1 \ 0 \\ 0 \ -1 \end{bmatrix} = \begin{bmatrix}0 \\ -1\end{bmatrix} = -\ket{1}$$
Swap Gate
A swap gate is used to swap the state of two qubits. It is denoted by the symbol:

If we order the states in the following sequence:
$$\ket{00}, \ket{01}, \ket {10}, \ket{11}$$
Then the swap gate is represented by the matrix:
$$SWAP= \begin{bmatrix}1 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 1 \ 0 \\ 0 \ 1 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 1\end{bmatrix}$$
In simple terms, if you have two qubits, one in state A and the other in state B, after applying the SWAP gate, the first qubit will be in state B and the second qubit will be in state A.
Observation / Measurement Gate
The observation gate (also called M-gate) is used to collapse the wave function. Once the qubit passes through that gate, it will effectively be reduced to a classical bit containing either the value of 0 or 1. One of the useful scenarios to use this gate is when the quantum part of your algorithm is over and you would like to get back to the classical computing part, using classical programming languages like C#. The observation gate uses the symbol:

Phase Gate (S)
The Phase Gate, often denoted as S, is a fundamental quantum gate that operates on a single qubit. It introduces a phase shift of π/2 to the state of a qubit. The matrix representation of the S gate is:
\(S=\begin{bmatrix} 1 \ 0 \\ 0 \ i \end{bmatrix}\)
This means that if a qubit is in the state |0>, the S gate leaves it unchanged. However, if the qubit is in the state |1>, the S gate adds a phase of π/2 to it. This phase shift is a unique quantum property that doesn’t have an analogue in classical computing. The S gate, along with other phase gates, plays a crucial role in many quantum algorithms where the relative phases of qubit states are used to manipulate and store information. It’s also a key component in creating more complex quantum gates and operations.
Square Root of NOT Gate
The Square Root of NOT Gate, often denoted as V, is a quantum gate that operates on a single qubit. It’s called the “square root” of NOT because applying it twice is equivalent to applying the NOT gate once. The matrix representation of the V gate is:
\(V=\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \ -1 \\ 1 \ 1 \end{bmatrix}\)
The Square Root of NOT Gate, or V gate, is like a magic trick with a coin.
Imagine you have a coin that can be in two states: heads (which we’ll call state |0>) and tails (state |1>). Now, the V gate is like a special flip of this coin. When you use the V gate (or do this special flip), the coin doesn’t just land on heads or tails. It lands in a state where it’s both heads and tails at the same time, but when you look at it (or measure it, in quantum terms), you’ll see either heads or tails, not both.
The interesting part is, if you do this special flip twice in a row (apply the V gate twice), it’s like doing a regular flip that only shows heads or tails. That’s why it’s called the “Square Root of NOT” gate.
CNOT Gate
A CNOT gate is an example of a gate that works on two qubits. It is also called a Controlled X Gate. It applies an X gate to one of the qubits only when the second one is set to 1. It is often used to implement entanglement. It is denoted with the following symbol:

CNOT gate is be used in calculations as a matrix:
$$\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}$$
Because the gate accepts two qubits as an input, it can operate on four combinations of states 0 and 1. The x operation is a tensor product that needs to be calculated first:
$$(\begin{bmatrix}1 \\ 0 \end{bmatrix}x\begin{bmatrix}1 \\ 0 \end{bmatrix})\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}= \begin{bmatrix}1 \\ 0 \\ 0 \\0 \end{bmatrix}\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}=\begin{bmatrix}1 \\ 0 \\ 0 \\ 0\end{bmatrix}=\begin{bmatrix}1 \\ 0 \end{bmatrix}x\begin{bmatrix}1 \\ 0 \end{bmatrix}$$
$$(\begin{bmatrix}1 \\ 0 \end{bmatrix}x\begin{bmatrix}0 \\ 1 \end{bmatrix})\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}= \begin{bmatrix}0 \\ 1 \\ 0 \\0 \end{bmatrix}\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}=\begin{bmatrix}0 \\ 1 \\ 0 \\ 0\end{bmatrix}=\begin{bmatrix}1 \\ 0 \end{bmatrix}x\begin{bmatrix}0 \\ 1 \end{bmatrix}$$
$$(\begin{bmatrix}0 \\ 1 \end{bmatrix}x\begin{bmatrix}1 \\ 0 \end{bmatrix})\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}= \begin{bmatrix}0 \\ 0 \\ 1 \\0 \end{bmatrix}\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}=\begin{bmatrix}0 \\ 0 \\ 0 \\ 1\end{bmatrix}=\begin{bmatrix}0 \\ 1 \end{bmatrix}x\begin{bmatrix}0 \\ 1 \end{bmatrix}$$
$$(\begin{bmatrix}0 \\ 1 \end{bmatrix}x\begin{bmatrix}0 \\ 1 \end{bmatrix})\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}= \begin{bmatrix}0 \\ 0 \\ 0 \\1 \end{bmatrix}\begin{bmatrix}1 0 0 0 \\ 0 1 0 0 \\ 0 0 0 1 \\ 0 0 1 0\end{bmatrix}=\begin{bmatrix}0 \\ 0 \\ 1 \\ 0\end{bmatrix}=\begin{bmatrix}0 \\ 1 \end{bmatrix}x\begin{bmatrix}1 \\ 0 \end{bmatrix}$$
The CNOT gate is often used to create entanglement, which is a quantum phenomenon where two qubits share a quantum state and become correlated. For example, applying a CNOT gate to two qubits that are both in the |+> state will result in the following entangled state:
CNOT( \(\ket{+}+\ket{+}\) )= \(\frac{1}{\sqrt{2}}(\ket{00}+\ket{01}+\ket{10}+\ket{11})=\frac{\ket{00}+\ket{11}}{\sqrt{2}}\)
where \(\ket{+} = \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\)
This state is also called a Bell state, and it has the property that measuring either qubit will reveal the state of the other qubit with certainty.
Conclusion
In this article, I have presented some of the basic quantum gates that are crucial for quantum computing. I have shown how they can be symbolized by symbols and matrices, and how they can change the qubit states. I have also demonstrated some examples of how quantum gates can produce superpositions, entanglement, and interference, which are the distinctive features of quantum computing. Quantum gates are the core of quantum algorithms, which can achieve faster or more optimal solutions to some problems than classical algorithms.
